وفي مقابل ذلك ، في حالة الجمع ، لا يهم الأمر على الإطلاق. ليس فقط في الرياضيات بل في الحياة العملية أيضًا ، فنحن نواجه هذين المفهومين بشكل منتظم. على الرغم من أننا لم نلاحظ ذلك. لذا ، خذ قراءة المقال بعناية ، لتعرف كيف يختلف هذان المفهومان.
رسم بياني للمقارنة
| أساس للمقارنة | تبديل | مزيج |
|---|---|---|
| المعنى | التقليب يشير إلى الطرق المختلفة لترتيب مجموعة من الكائنات بترتيب تسلسلي. | يشير المزيج إلى عدة طرق لاختيار العناصر من مجموعة كبيرة من الكائنات ، بحيث لا يهم ترتيبها. |
| طلب | ذو صلة | ليست له صلة، لا علاقة له مع الموضوع |
| ترمز | ترتيب | اختيار |
| ما هذا؟ | العناصر المطلوبة | مجموعات غير مرتبة |
| الأجوبة | كم ترتيب مختلف يمكن إنشاؤه من مجموعة معينة من الأشياء؟ | كم عدد المجموعات المختارة التي يمكن اختيارها من مجموعة أكبر من الكائنات؟ |
| استنتاج | متعددة التقليب من مجموعة واحدة. | مزيج واحد من التقليب واحد. |
تعريف التقليب
نحن نعرّف التباين بطرق مختلفة لترتيب بعض أو جميع أعضاء مجموعة ما بترتيب معين. إنه يتضمن كل الترتيبات الممكنة أو إعادة ترتيب المجموعة المعينة ، إلى ترتيب مميز.
على سبيل المثال ، كل التجليد المحتمل الذي تم إنشاؤه بالحروف x، y، z -
- من خلال اتخاذ كل ثلاثة في وقت واحد هي xyz ، xzy ، yxz ، yzx ، zxy ، zyx.
- من خلال أخذ اثنين في كل مرة xy ، xz ، yx ، yz ، zx ، zy.
يمكن حساب إجمالي عدد التباديل المحتمل للأشياء n ، التي تم التقاطها r في كل مرة ، على النحو التالي:
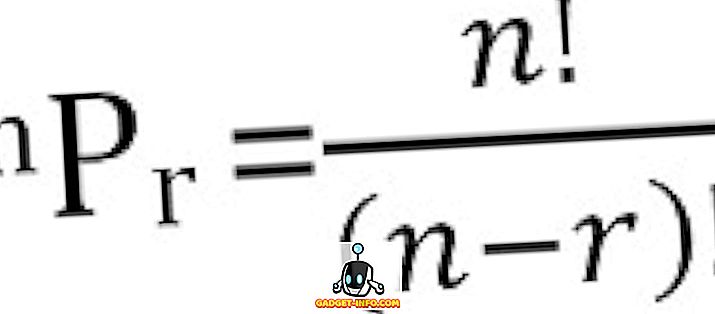
تعريف الدمج
يتم تعريف المجموعة على أنها الطرق المختلفة ، واختيار مجموعة ، عن طريق أخذ بعض أو جميع أعضاء مجموعة ، دون الترتيب التالي.
على سبيل المثال ، جميع المجموعات الممكنة المختارة بحرف m ، n ، o -
- عندما يتم اختيار ثلاثة من أصل ثلاثة أحرف ، فإن المجموعة الوحيدة هي mno
- عندما يتم اختيار حرفين من أصل ثلاثة أحرف ، فإن المجموعات المحتملة تكون mn ، no ، om.
يمكن حساب إجمالي عدد المجموعات الممكنة من n الأشياء ، التي اتخذت في وقت واحد على النحو التالي:
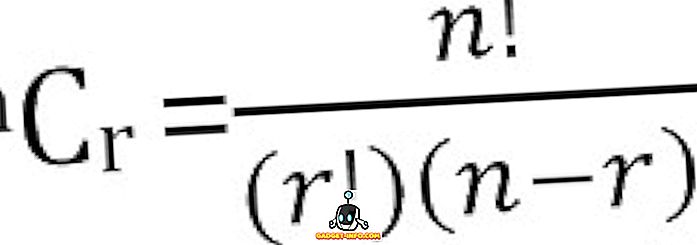
الاختلافات الرئيسية بين التقليب والجمع
يتم رسم الاختلافات بين التقليب والجمع بوضوح على الأسس التالية:
- يشير مصطلح التقديم إلى عدة طرق لترتيب مجموعة من الكائنات بترتيب تسلسلي. يتضمن الدمج عدة طرق لاختيار العناصر من مجموعة كبيرة من الكائنات ، بحيث لا يكون ترتيبها غير ذي صلة.
- النقطة المميزة الأساسية بين هذين المفهومين الرياضيين هي الترتيب ، والموضع ، والموضع ، أي في خصائص التقليب المذكورة أعلاه ، الأمر الذي لا يهم في حالة الجمع.
- يشير التحويل إلى عدة طرق لترتيب الأشياء ، والأشخاص ، والأرقام ، والحروف الأبجدية ، والألوان ، وما إلى ذلك. وعلى الجانب الآخر ، تشير المجموعة إلى طرق مختلفة لاختيار عناصر القائمة ، الطعام ، الملابس ، الموضوعات ، إلخ.
- التجليد ليس سوى تركيبة مرتبة بينما يتضمن Combination مجموعات غير مرتبة أو اقتران قيم ضمن معايير محددة.
- يمكن اشتقاق العديد من التباديل من مجموعة واحدة. على العكس ، يمكن الحصول على مجموعة واحدة فقط من التقليب الواحد.
- إجابات التقليب كم عدد الترتيبات المختلفة التي يمكن إنشاؤها من مجموعة معينة من الكائنات؟ على عكس المجموعة التي تشرح كيف يمكن اختيار مجموعات مختلفة من مجموعة كبيرة من الأشياء؟
مثال
لنفترض أن هناك حالة حيث يجب عليك معرفة العدد الإجمالي للعينات الممكنة لسببين من أصل ثلاثة كائنات أ ، ب ، ج. في هذا السؤال ، أولاً وقبل كل شيء ، يجب أن تفهم ، ما إذا كان السؤال يتعلق بالتبديل أو الجمع والطريقة الوحيدة للعثور على ذلك هي التحقق مما إذا كان الطلب مهمًا أم لا.
إذا كان الطلب مهمًا ، فإن السؤال يتعلق بالتعديل ، والعينات الممكنة ستكون ، AB ، BA ، BC ، CB ، AC ، CA. حيث يختلف AB عن BA ، يختلف BC عن CB و AC مختلف.
إذا كان الأمر غير ذي صلة ، فإن السؤال مرتبط بالمجموعة ، وستكون العينات الممكنة AB و BC و CA.
استنتاج
مع المناقشة أعلاه ، من الواضح أن التقليب والجمع بين المصطلحات المختلفة ، والتي تستخدم في الرياضيات والإحصاءات والأبحاث وحياة اليوم. من النقاط التي يجب تذكرها ، فيما يتعلق بهذين المفهومين ، أنه ، بالنسبة لمجموعة معينة من الكائنات ، سيكون التغيير دائمًا أعلى من مجموعته.