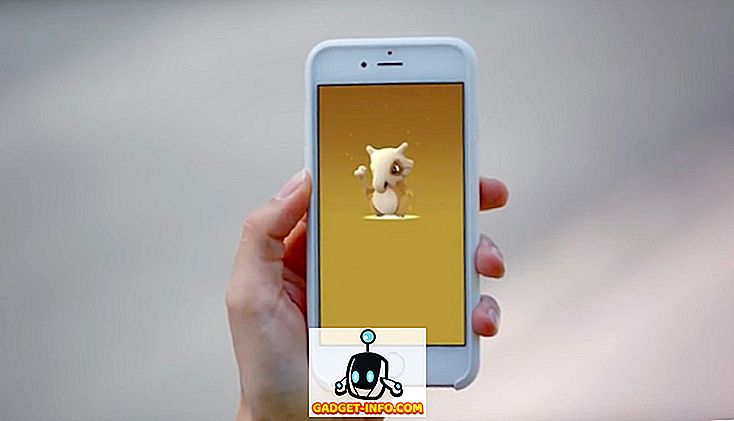
لاختبار الفرضية ، مطلوب إحصائيات الاختبار ، والتي تتبع توزيع معروف. في الاختبار ، هناك قسمان لمنحنى كثافة الاحتمال ، أي منطقة القبول ومنطقة الرفض. تسمى منطقة الرفض كمنطقة حرجة .
في مجال الأبحاث والتجارب ، من المفيد معرفة الفرق بين اختبار الذيل الواحد والذيل ثنائي الذيل ، حيث إنهما شائعان الاستخدام في العملية.
رسم بياني للمقارنة
| أساس المقارنة | اختبار واحد الذيل | اختبار ثنائي الذيل |
|---|---|---|
| المعنى | يُعرف اختبار فرضيّة احصائيّة فيها فرضية بديلة لنهاية واحدة فقط ، ويعرف باختبار اختبار الذيل. | يُعرف اختبارًا مهمًا في فرضية بديلة بنهايتين ، باسم اختبار ثنائي الذيل. |
| فرضية | اتجاهي | غير موجه |
| منطقة الرفض | إما يسارًا أو يمينًا | كلا اليسار واليمين |
| يحدد | إذا كانت هناك علاقة بين المتغيرات في اتجاه واحد. | إذا كانت هناك علاقة بين المتغيرات في أي من الاتجاهين. |
| نتيجة | أكبر أو أقل من قيمة معينة. | أكبر أو أقل من مجموعة معينة من القيم. |
| تسجيل الدخول في فرضية بديلة | > أو | ≠ |
تعريف اختبار واحد الذيل
يلمح الاختبار أحادي الطرف إلى اختبار الأهمية الذي تظهر فيه منطقة الرفض في نهاية توزيع العينة. وهو يشير إلى أن معلمة الاختبار المقدرة أكبر أو أقل من القيمة الحرجة. عندما يقع اختبار العينة في منطقة الرفض ، أي الجانب الأيسر أو الأيمن ، حسب الحالة ، يؤدي ذلك إلى قبول فرضية بديلة بدلاً من فرضية العدم. يتم تطبيقه في المقام الأول في توزيع مربع كاي ؛ التي تتحقق من صلاح صالح.
في هذا الاختبار الفرضي الإحصائي ، يتم وضع كل المنطقة الحرجة ، المرتبطة بـ α ، في أي من الذيلان. يمكن أن يكون الاختبار أحادي الطرف:
- اختبار الذيل الأيسر : عندما يعتقد أن معلمة السكان أقل من المفترض ، فإن اختبار الفرضية الذي يتم إجراؤه هو اختبار الطرف الأيسر.
- اختبار الذيل الأيمن : عندما يفترض أن تكون معلمة السكان أكبر من القيمة المفترضة ، فإن الاختبار الإحصائي الذي يتم إجراؤه هو اختبار ذو الطرف الأيمن.
تعريف اختبار ثنائي الذيل
يوصف الاختبار ثنائي الذيل بأنه اختبار فرضي ، حيث تكون منطقة الرفض أو المنطقة الحرجة على طرفي التوزيع الطبيعي. يحدد ما إذا كان اختبار العينة يقع داخل أو خارج نطاق معين من القيم. لذلك ، يتم قبول فرضية بديلة بدلاً من الفرضية الصفرية ، إذا كانت القيمة المحسوبة تقع في أي من ذيلتي توزيع الاحتمال.
في هذا الاختبار ، يتم تقسيم α إلى جزأين متساويين ، وضع النصف على كل جانب ، أي أنه يعتبر إمكانية كل من التأثيرات الإيجابية والسلبية. يتم تنفيذه لمعرفة ما إذا كانت المعلمة المقدرة إما أعلى أو أقل من المعلمة المفترضة ، بحيث تعمل القيم المتطرفة كدليل ضد فرضية العدم.
الاختلافات الرئيسية بين واحد الذيل واختبار ثنائي الطرف
يتم شرح الاختلافات الأساسية بين اختبار الذيل الواحد والمختبرين في النقاط التالية:
- الاختبار أحادي الطرف ، كما يوحي الاسم هو اختبار الفرضية الإحصائية ، حيث يكون للفرضية البديلة نهاية واحدة. من ناحية أخرى ، فإن الاختبار ثنائي الذيل ينطوي على اختبار الفرضية. حيث أن الفرضية البديلة لها نهايات مزدوجة.
- في الاختبار أحادي الطرف ، يتم تمثيل فرضية بديلة بشكل مباشر. وعلى العكس ، فإن الاختبار ثنائي الطرف هو اختبار فرضية غير اتجاهية.
- في اختبار أحادي الطرف ، تكون منطقة الرفض إما على يسار أو يمين توزيع العينات. على العكس ، فإن منطقة الرفض تكون على جانبي توزيع العينة.
- يستخدم اختبار أحادي الطرف للتأكد من وجود أي علاقة بين المتغيرات في اتجاه واحد ، أي اليسار أو اليمين. في مقابل ذلك ، يتم استخدام الاختبار ثنائي الطرف لتحديد ما إذا كانت هناك أي علاقة بين المتغيرات في أي اتجاه.
- في اختبار أحادي الطرف ، تكون معلمة الاختبار محسوبة أكثر أو أقل من القيمة الحرجة. على خلاف الاختبار ثنائي الطرف ، فإن النتيجة التي يتم الحصول عليها تكون ضمن قيمة حرجة أو خارجها.
- عندما يكون للفرضية البديلة علامة "≠" ، يتم إجراء اختبار ثنائي الذيل. في المقابل ، عندما تكون هناك فرضية بديلة تحتوي على "> أو" ، يتم إجراء اختبار الذيل الواحد.
استنتاج
باختصار ، يمكننا أن نقول أن الفرق الأساسي بين اختبار الذيل الواحد والذيل ثنائي الذيل يكمن في الاتجاه ، أي في حالة ما إذا كانت فرضية البحث تستلزم اتجاه الترابط أو الاختلاف ، عندئذٍ يتم تطبيق اختبار الذيل الواحد ، ولكن إذا لا تعني فرضية البحث اتجاه التفاعل أو الاختلاف ، فنحن نستخدم اختبار ثنائي الطرف.