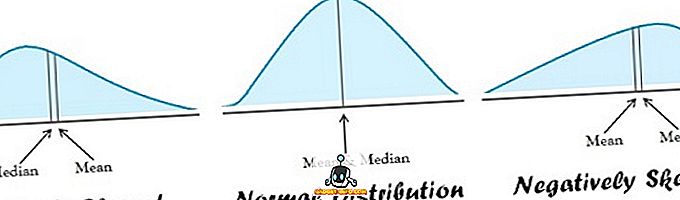
المقياس المثالي للاتجاه المركزي هو المقياس المحدد بوضوح ، والمفهوم بسهولة ، وهو ببساطة قابل للحساب. يجب أن يعتمد على جميع الملاحظات والأقل تأثرًا بالملاحظات المتطرفة الموجودة في مجموعة البيانات.
غالبًا ما يتباين الناس بين هاتين المقياسين ، لكن الحقيقة هي أنهم مختلفون. توضح هذه المقالة بشكل خاص الاختلافات الأساسية بين المتوسط والوسيط. الق نظرة.
رسم بياني للمقارنة
| أساس للمقارنة | تعني | الوسيط |
|---|---|---|
| المعنى | يعني المتوسط البسيط للمجموعة المحددة من القيم أو الكميات. | يُعرَّف الوسيط بأنه الرقم الأوسط في قائمة قيم مرتبة. |
| ما هذا؟ | إنه متوسط حسابي. | إنه متوسط الموقع. |
| يمثل | مركز ثقل مجموعة البيانات | مركز ثقل مجموعة البيانات نقطة منتصف مجموعة البيانات |
| القابلية للتطبيق | التوزيع الطبيعي | توزيع الانحراف |
| ايسكنون | يعني حساس للقيم المتطرفة. | Median ليست حساسة للمغتربين. |
| عملية حسابية | يتم حساب المتوسط عن طريق إضافة جميع الملاحظات ثم تقسيم القيمة التي تم الحصول عليها مع عدد المشاهدات. | لحساب المتوسط ، يتم ترتيب مجموعة البيانات بترتيب تصاعدي أو تنازلي ، ثم تكون القيمة التي تقع في منتصف مجموعة البيانات الجديدة ، هي الوسيط. |
تعريف المتوسط
المتوسط هو المقياس المستخدم على نطاق واسع للميل المركزي ، والذي يعرف كمتوسط مجموعة القيم. وهو يمثل النموذج والقيمة الأكثر شيوعًا لنطاق القيم المعطى. يمكن حسابه ، سواء في سلسلة منفصلة ومتواصلة.
المتوسط يساوي مجموع كل الملاحظات مقسومًا على عدد المشاهدات في مجموعة البيانات. إذا كانت القيمة المفترضة بواسطة متغير متساوية ، فسيكون متوسطها أيضًا. يمكن أن يكون المتوسط من نوعين ، متوسط العينة (x̅) ومتوسط عدد السكان (µ). يمكن حسابه مع صيغة معينة:
- المتوسط الحسابي :

ن = عدد القيم - للسلسلة المنفصلة :

- لخدمة مستمرة :

أ = متوسط مفترض
C = القاسم المشترك
تعريف الوسيط
المتوسط هو مقياس مهم آخر للاتجاه المركزي ، يستخدم لتقسيم القيمة إلى قسمين متساويين ، أي نصف أكبر من العينة ، أو التوزيع السكاني أو الاحتمالي من النصف السفلي. إنها القيمة المتوسطة الأكبر ، والتي تتحقق عندما يتم فرز الملاحظات بترتيب معين ، إما ترتيب تصاعدي أو تنازلي.
لحساب الوسيط ، أولا وقبل كل شيء ، ترتيب الملاحظات في أدنى إلى أعلى أو أعلى إلى أدنى ، ثم تطبيق الصيغة المناسبة ، وفقا للشروط الواردة أدناه:
- إذا كان عدد المشاهدات غريبًا :

- إذا كان عدد المشاهدات حتى :

- للسلسلة المستمرة :

c = التكرار التراكمي للفئة المتوسطة السابقة
و = تردد الطبقة المتوسطة
h = عرض الفصل
الاختلافات الرئيسية بين المتوسط والوسيط
يتم توفير الاختلافات الهامة بين المتوسط والوسيط في المادة أدناه:
- في الإحصائيات ، يُعرّف المتوسط بأنه المتوسط البسيط لمجموعة معينة من القيم أو الكميات. ويقال إن الوسيط هو الرقم الأوسط في قائمة قيم مرتبة.
- في حين أن متوسط المتوسط الحسابي ، فإن الوسيط هو متوسط الموضع ، في جوهره ، يحدد موضع مجموعة البيانات قيمة الوسيط.
- يشير المتوسط إلى مركز ثقل مجموعة البيانات بينما يسلط الوسيط الضوء على القيمة المتوسطة لمعظم مجموعة البيانات.
- الوسط مناسب للبيانات الموزعة بشكل طبيعي. على الطرف الآخر ، يكون الوسيط هو الأفضل عندما يكون توزيع البيانات منحرفًا.
- يتأثر المتوسط بشدة بالقيمة القصوى التي ليست في حالة الوسيط.
- يتم حساب المتوسط عن طريق إضافة جميع الملاحظات ثم تقسيم القيمة التي تم الحصول عليها مع عدد الملاحظات ؛ والنتيجة هي يعني. على العكس من الوسيط ، يتم ترتيب مجموعة البيانات بترتيب تصاعدي أو تنازلي ، ثم تكون القيمة التي تقع في منتصف مجموعة البيانات الجديدة هي الوسيط.
مثال
العثور على متوسط ومتوسط مجموعة البيانات المعطاة:
58 و 26 و 65 و 34 و 78 و 44 و 96
الحل: لحساب متوسط ، تحتاج إلى تقسيم مجموع الملاحظات مع عدد الملاحظات ،

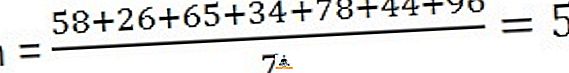
لحساب المتوسط ، أولاً ، قم بترتيب السلسلة في تسلسل ، أي أدنى إلى أعلى ،
26 و 34 و 44 و 58 و 65 و 78 و 96
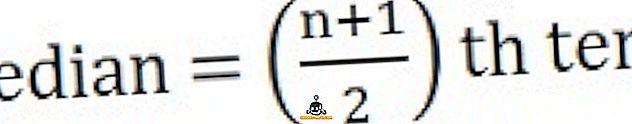
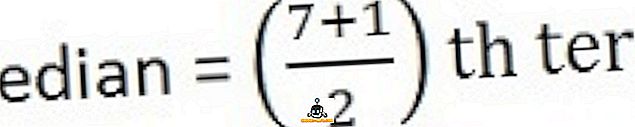
استنتاج
بعد مراجعة النقاط المذكورة أعلاه ، يمكننا القول أن هذين المفهومين الرياضيين مختلفان. يعتبر المتوسط الحسابي أو المتوسط أفضل مقياس للميل المركزي حيث أنه يحتوي على جميع ميزات المقياس المثالي ولكن له عيب بأن تقلبات أخذ العينات تؤثر على المتوسط.
وبنفس الطريقة ، يتم تعريف الوسيط أيضًا بشكل لا لبس فيه ومن السهل فهمه وحسابه ، وأفضل شيء في هذا الإجراء هو أنه لا يتأثر بتقلبات أخذ العينات ، ولكن العيب الوحيد في المتوسط هو أنه لا يعتمد على جميع الملاحظات. لتصنيف نهاية مفتوحة ، يفضل المتوسط عادة على الوسط.















