يمكن وصف قائمة الانتظار على أنها بنية بيانات خطية غير بدائية تتبع ترتيب FIFO الذي يتم فيه إدخال عناصر البيانات من الطرف الواحد (الطرف الخلفي) ويتم حذفها من الطرف الآخر (الواجهة الأمامية). الاختلافات الأخرى في قائمة الانتظار هي قائمة الانتظار الدائرية ، قائمة انتظار نهاية مضاعف وقائمة انتظار الأولوية.
رسم بياني للمقارنة
| أساس للمقارنة | الطابور الخطي | قائمة انتظار دائري |
|---|---|---|
| الأساسية | ينظم عناصر البيانات والإرشادات بترتيب تسلسلي واحد بعد الآخر. | يرتب البيانات في النمط الدائري حيث يتم توصيل العنصر الأخير بالعنصر الأول. |
| ترتيب تنفيذ المهمة | يتم تنفيذ المهام حتى يتم وضعها قبل (FIFO). | قد يتم تغيير ترتيب تنفيذ مهمة. |
| الإدراج والحذف | يتم إضافة العنصر الجديد من النهاية الخلفية وإزالته من الأمام. | الإدراج والحذف يمكن القيام به في أي موقف. |
| أداء | غير فعال | يعمل بشكل أفضل من قائمة الانتظار الخطية. |
تعريف الطابور الخطي
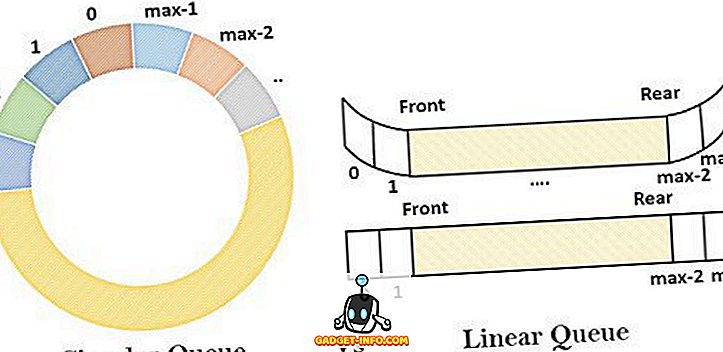
الطابور الخطي هو ، بعقلانية ، الأول في القائمة المرتبة الأولى . يطلق عليه خطي لأنه يشبه إلى خط مستقيم حيث يتم وضع العناصر واحدة تلو الأخرى. يحتوي على مجموعة متجانسة من العناصر التي يتم فيها إضافة عناصر جديدة في نهاية واحدة وحذفها من طرف آخر. يمكن فهم مفهوم الطابور على سبيل المثال من قائمة انتظار الجمهور المنتظرين خارج مكتب التذاكر للحصول على تذكرة المسرح. في هذا الطابور ، ينضم الشخص إلى الطرف الخلفي من قائمة الانتظار لأخذ التذكرة ويتم إصدار التذكرة في الواجهة الأمامية من قائمة الانتظار.
هناك العديد من العمليات التي يتم تنفيذها في قائمة الانتظار
- أولاً يتم تهيئة قائمة الانتظار إلى صفر (أي فارغة).
- تحديد ما إذا كانت قائمة الانتظار فارغة أم لا.
- تحديد ما إذا كانت قائمة الانتظار ممتلئة أم لا.
- إدخال العنصر الجديد من النهاية الخلفية (Enqueue).
- حذف العنصر من الواجهة الأمامية (Dequeue).
يمكن تنفيذ قائمة الانتظار بطريقتين
- بشكل ثابت (باستخدام المصفوفات)
- بشكل حيوي (استخدام المؤشرات)
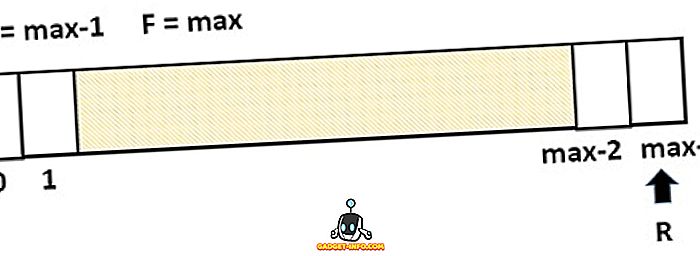
الحد من قائمة الانتظار الخطية هو أنه ينشئ سيناريو حيث لا يمكن إضافة عنصر جديد في قائمة الانتظار حتى إذا احتوت قائمة الانتظار على مسافات فارغة. هذا الوضع أعلاه موضح في الشكل أدناه. هنا يشير المؤخر إلى المؤشر الأخير في حين أن جميع الصناديق فارغة ، ولا يمكن إضافة عنصر جديد.
تعريف قائمة الانتظار الدائرية
الطابور الدائري هو متغير من الطابور الخطي الذي يتغلب بشكل فعال على الحد لقائمة الانتظار الخطية. في الطابور الدائري ، تتم إضافة العنصر الجديد في الموضع الأول لقائمة الانتظار إذا كان الأخير مشغولًا والمساحة متوفرة. عندما يتعلق الأمر بطابور خطي ، لا يمكن تنفيذ الإدراج إلا من الطرف الخلفي والحذف من الواجهة الأمامية. في قائمة انتظار كاملة بعد تنفيذ سلسلة من عمليات الحذف المتتالية في قائمة الانتظار ، تنشأ حالة معينة حيث لا يمكن إضافة عنصر جديد أكثر حتى إذا كانت المساحة المتاحة لأن شرط Underflow (Rear = max - 1) لا يزال موجودًا.
تعمل قائمة الانتظار الدائرية على الربط بين الطرفين من خلال مؤشر حيث يأتي العنصر الأول بعد العنصر الأخير. كما أنه يتتبع من الأمام والخلف عن طريق تطبيق بعض المنطق الإضافي بحيث يتمكن من تتبع العناصر التي سيتم إدراجها وحذفها. مع هذا ، لا تنشئ قائمة الانتظار الدائرية شرط تجاوز السعة حتى قائمة كاملة في الفعلي.
بعض الشروط يتبعها الطابور الدائري:
- الجبهة يجب أن تشير إلى العنصر الأول.
- ستكون قائمة الانتظار فارغة إذا كانت Front = Rear.
- عند إضافة عنصر جديد يتم زيادة قائمة الانتظار حسب القيمة الأولى (Rear = Rear + 1).
- عند حذف عنصر من قائمة الانتظار ، تتم زيادة الواجهة بأحدها (Front = Front + 1).
الاختلافات الرئيسية بين قائمة الانتظار الخطية و Queular Queue
- قائمة الانتظار الخطية هي قائمة مرتبة حيث يتم تنظيم عناصر البيانات بالترتيب التسلسلي. في المقابل ، يخزن الطابور الدائري البيانات بطريقة دائرية.
- تتبع الطابور الخطي ترتيب FIFO لتنفيذ المهمة (سيتم حذف العنصر المضاف في الموضع الأول في الموضع الأول). على العكس ، في الطابور الدائري ، قد يتغير ترتيب العمليات التي يتم تنفيذها على عنصر ما.
- يتم تثبيت الإدراج وحذف العناصر في طابور خطي ، أي الإضافة من النهاية الخلفية والحذف من الواجهة الأمامية. من ناحية أخرى ، فإن الطابور الدائري قادر على إدخال وحذف العنصر من أي نقطة إلى أن يكون غير مشغول.
- يهدر الطابور الخطي مساحة الذاكرة بينما يجعل الطابور الدائري الاستخدام الفعال للمساحة.
تنفيذ الطابور الخطي
توضح الخوارزمية الموضحة أدناه إضافة عناصر في قائمة الانتظار:
تحتاج قائمة الانتظار إلى ثلاثة متغيرات للبيانات بما في ذلك صفيف واحد لتخزين قائمة الانتظار وغيرها لتخزين الوضع الأولي الأمامي والخلفي الذي هو -1.
insert (item، queue، n، rear) {if (rear == n) ثم اطبع "تجاوز قائمة الانتظار"؛ else {rear = rear + 1؛ قائمة الانتظار [الخلفية] = البند ؛ }} توضح الخوارزمية الموضحة أدناه حذف العناصر في قائمة الانتظار:
delete_circular (item، queue، rear، front) {if (rear == front) then then "queue underflow"؛ else {front = front + 1؛ item = queue [front]؛ }} تنفيذ الطابور الدائري
خوارزمية لتفسير إضافة العنصر في الطابور الدائري:
insert_circular (item، queue، rear، front) {rear = (rear + 1) mod n؛ إذا كانت (front == rear) ثم طباعة "قائمة الانتظار ممتلئة"؛ else {queue [rear] = item؛ }} توضح الخوارزمية حذف العنصر في قائمة الانتظار الدائرية:
delete_circular (item، queue، rear، front) {if (front == rear) then print ("queue is empty")؛ else {front = front + 1؛ item = queue [front]؛ }} استنتاج
الطابور الخطي غير فعال في حالات معينة حيث تكون العناصر مطلوبة للانتقال إلى المساحات الخالية من أجل تنفيذ عملية الإدراج. هذا هو السبب في أنه يميل إلى إهدار مساحة التخزين في حين أن الطابور الدائري يجعل الاستخدام المناسب لمساحة التخزين حيث تتم إضافة العناصر في أي موضع إذا كان هناك مساحة فارغة.